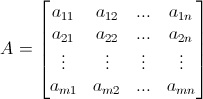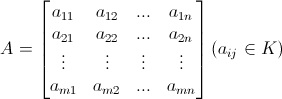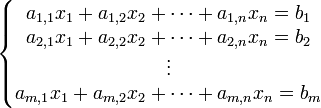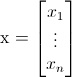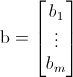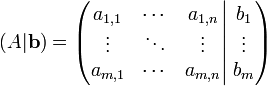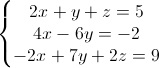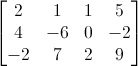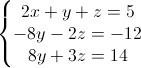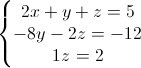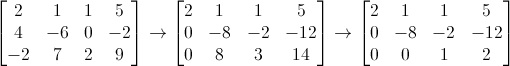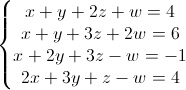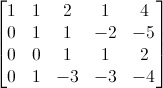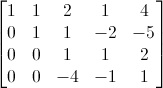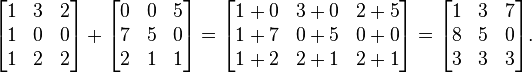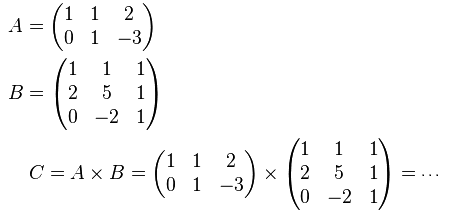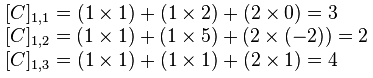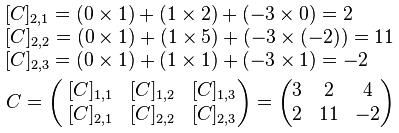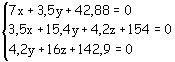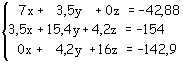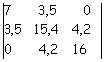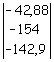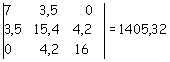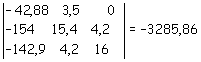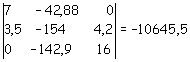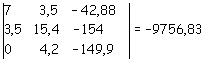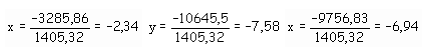To totally unlock this section you need to Log-in
Login
Una matrice m x n (m righe per n colonne) e' una tabella come la seguente:
A questo punto daremo una definizione più corretta alle matrici:
Le matrici sono degli insiemi di numeri (od elementi) disposti in modo "rettangolare" (o quadrangolare, in quanto le matrici possono anche "quadrate"). Possiamo immaginare le matrici come delle tabelle con numero di righe e colonne arbitrario.
Una matrice A di tipo (m,n) (possiamo anche chiamarla matrice m × n) con m,n interi positivi, a elementi in un campo K è una tabella rettangolare di numeri disposti in m righe e n colonne:
aij è il numero che si trova sulla i-esima riga e sulla j-esima colonna di A.
In termini più rigorosi si dice che aij è l'elemento di posto (i, j) della matrice A.
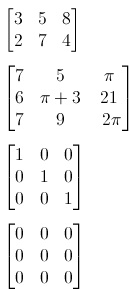
In particolare, nel secondo caso abbiamo di fronte una matrice quadrata (presenta lo stesso numero di righe e colonne), nel terzo caso abbiamo una matrice unità (o matrice identità o matrice identica) e nel quarto caso una matrice nulla (o matrice zero, tutti gli elementi sono valorizzati a 0).
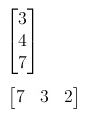
La prima matrice, costituita da 3 righe e da una sola colonna, è un esempio di vettore colonna, mentre la seconda matrice, formata da 3 colonne e una riga, rappresenta un caso di vettore riga.
Il metodo Gauss-Jordan
Detto ciò, sorge una domanda, che cos'è il metodo di Gauss-Jordan?
Il metodo (di eliminazione) di Gauss-Jordan non è altro che un importante metodo (dell'algebra lineare) di risoluzione dei sistemi di equazioni, il quale sfrutta pure le sopracitate matrici! Consideriamo quindi un generico sistema di equazioni lineari:
NOTA: ricordiamo che un'equazione lineare, o equazione di primo grado, è un'equazione algebrica di primo grado, dove cioè il grado massimo, o grado polinomiale, delle incognite presenti nell'equazione (che possono essere molteplici) è uno.
Consideriamo quindi un generico sistema di equazioni lineari:
Esso è un sistema di m equazioni lineari nelle n incognite X1,...,Xn.
Il sistema viene definito omogeneo se b1 = b2 = ... = bm = 0. In caso contrario, il sistema è ovviamente detto non omogeneo.
Dal sistema, ovvero dall'insieme di equazioni proposte, possiamo ricavare una particolare matrice, denominata matrice dei coefficienti A:
Adesso raggruppiamo le incognite per formare il vettore x delle incognite:
Ed infinepure i termini noti per costituire il vettore b dei termini noti:
Si può inoltre definire la matrice completa (o orlata), ottenuta aggiungendo ad A il vettore colonna b:
Per indicare in maniera semplice il sistema possiamo pertanto utilizzare l'espressione Ax = b.
Ad esempio, prendendo il sistema:
Otteniamo la matrice completa:
Abbiamo dunque visto che qualunque sistema di equazioni lineari può essere trascritto in una matrice orlata (e viceversa).
Risoluzione col metodo di Gauss-Jordan
Ma come si risolve un sistema? Un procedimento di risoluzione è appunto l'algoritmo di Gauss-Jordan.
Il suddetto metodo consente infatti di stabilire se il sistema risulta compatibile (ovvero se ammette soluzioni) oppure no, e nel caso sussistano soluzioni, permette di trovarle tutte.
Il procedimento consiste nel sostituire il sistema dato con un sistema "triangolare" ad esso equivalente, ottenuto tramite una serie di passaggi chiamati "operazioni elementari sulle equazioni del sistema".
Tali operazioni corrispondono ad altrettante operazioni sulle righe della matrice completa. Ergo, osserviamo quali sono le operazioni elementari che si possono attuare sulle equazioni di un sistema:
1) scambiare fra loro 2 equazioni del sistema;
2) moltiplicare (primo e secondo membro) di un'equazione per uno stesso scalare non nullo;
3) sostituire un'equazione con quella ottenuta sommando ad essa un multiplo di un'altra equazione.
Queste operazioni si possono tradurre, nell'ambito delle matrici, come operazioni sulle righe di una matrice:
1) scambiare tra loro 2 righe della matrice;
2) moltiplicare una riga della matrice per uno scalare non nullo;
3) sostituire una riga della matrice con quella ottenuta sommando ad essa un multiplo di un'altra riga.
Pertanto, trattasi di operazioni veramente semplici da comprendere e da attuare. Ora mettiamo in pratica il metodo di Gauss-Jordan: riprendiamo il sistema precedente:
Dobbiamo ottenere, mediante le operazioni elementari elencate sopra, un sistema che permetta una "sostituzione all'indietro", cioè un sistema che nella prima equazione presenti tutte e 3 le incognite (x,y,z), nella seconda equazione 2 incognite (y,z) e nella terza un'incognita (z), in questo modo sarà possibile, facilmente, tornare a ritroso nelle restanti equazioni lineari e risolvere il sistema.
Abbiamo il sistema; il nostro primo obiettivo è quello di eliminare x dalla seconda e terza equazione. Come facciamo?
Semplice: utilizziamo le operazioni elementari.
Dunque, sottraiamo 2 volte la prima equazione dalla seconda e sottraiamo -1 volte la prima equazione dalla terza.
Otteniamo così il sistema equivalente:
Il coefficiente 2 della prima equazione si dice primo pivot.
Abbiamo eliminato la x dalla seconda e terza equazione: adesso dobbiamo eliminare la y dalla terza equazione. A tal scopo sottraiamo -1 volte la seconda equazione dalla terza:
Il coefficiente -8 della seconda equazione è chiamato secondo pivot, mentre il coefficiente 1 della terza equazione è detto terzo pivot. Finalmente siamo giunti ad un sistema equivalente (in una forma "triangolare) che ci permette di trovare le soluzioni sostituendo all'indietro.
Alla fine le soluzioni sono: z = 2, y = 1, x = 1. Lo stesso però si può fare in maniera molto più rapida sfruttando le matrici. Riprendiamo la matrice completa associata al sistema di partenza:
Il nostro obiettivo sarà rendere 0 il primo valore della seconda riga, e rendere 0 i primi 2 valori della terza riga, ovviamente attraverso le operazioni elementari sulle righe.
Non abbiamo fatto altro che lo stesso procedimento di prima, questa volta, tuttavia, con le matrici, ottenendo una matrice a gradini (o a scala).
Se volete la conferma che il risultato è lo stesso, riscrivete l'ultima matrice sotto forma di sistema e vedrete che è esattamente uguale a quello da cui abbiamo ricavato le soluzioni (z = 2, y = 1, x = 1) in precedenza.
Facciamo un ulteriore esempio, questa volta con un sistema avente 4 equazioni e 4 incognite:
Procediamo direttamente con il metodo di Gauss-Jordan per le matrici; ergo, scriviamo la matrice completa:
La prima cosa da fare è far diventare 0 il primo termine della seconda riga: addizioniamo la seconda riga con la prima riga moltiplicata per -1:
Ora, cerchiamo di far diventare 0 il primo elemento della terza riga, sommando -1 volte la prima riga alla terza riga:
Adesso possiamo fare una bella e assai conveniente cosa: scambiamo fra loro la seconda e la terza riga:
Ora dobbiamo solamente sistemare l'ultima riga: innanzitutto sommiamo -2 volte la prima riga alla quarta riga:
Dopodiché, sommiamo -1 volte la seconda riga alla quarta:
Infine, sommiamo 4 volte la terza riga alla quarta riga:
Abbiamo in questo modo ottenuto una matrice a gradini (o triangolare)!
Scrivendo il sistema associato e risolvendo con sostituzione all'indietro otteniamo i risultati:
w = 3;
z = -1;
y = 2;
x = 1
Riassumendo, come abbiamo potuto constatare, il metodo di Gauss-Jordan è sicuramente molto utile nella risoluzione di sistemi di equazioni, anche se, come tutti i metodi, ha i suoi pro e contro!
Chi era Jordan?
Wilhelm Jordan (1842-1899), nacque a Ellwangen, una piccola città nel sud della Germania. Egli studiò all'istituto politecnico di Stoccarda.
Successivamente al lavoro, della durata di 2 anni, in veste di assistente ingegnere alle fasi preliminari della costruzione delle ferrovie, ritornò nel 1865 a Stoccarda come assistente in geodesia.
Dal 1881 fino alla sua morte fu professore di geodesia e geometria pratica all'università di Hannover. Scrisse un manuale di geodesia (Handbuch der Vermessungskunde), rappresentante la sua opera più famosa.
L'algoritmo di Gauss-Jordan apparve nel 1888 nella terza edizione del suo manuale di geodesia.
Qual è il miglioramento apportato da Jordan al metodo tradizionale di Gauss? Ebbene, Jordan ha fatto sì che il procedimento consenta di calcolare anche l'inversa di una matrice.
A tal proposito ricordiamo che una matrice quadrata A (stesso numero di righe e colonne) si dice invertibile se esiste una matrice M tale che AM = MA = I, dove I è la matrice identità.
Se esiste, M è unica ed è chiamata inversa di A, denotandola con la notazione A−1.
Algebra delle matrici
Sulle matrici si possono definire numerose operazioni: due matrici (aventi dei numeri opportuni di righe e colonne) possono essere sommate, sottratte, moltiplicate fra loro, e moltiplicate per un numero (detto scalare).
Somma
Due matrici A e B , entrambe di tipo M x N, possono essere sommate. La loro somma A+B è definita come la matrice M x N i cui elementi sono ottenuti sommando i corrispettivi elementi di A e B . Formalmente:
Per esempio:
Moltiplicazione per uno scalare
La moltiplicazione per uno scalare è un'operazione che, data una matrice A ed un numero c (detto scalare), costruisce una nuova matrice c x A, il cui elemento è ottenuto moltiplicando l'elemento corrispondente di A per c ; la matrice e lo scalare scelti devono appartenere allo stesso campo (ovvero numeri naturali, razionali, reali, etc.). Formalmente:
Per esempio:
Prodotto
La moltiplicazione tra due matrici A e B è un'operazione più complicata delle precedenti. A differenza della somma, non è definita moltiplicando semplicemente gli elementi aventi lo stesso posto. La definizione di moltiplicazione che segue è motivata dal fatto che una matrice modellizza una applicazione lineare, e in questo modo il prodotto di matrici corrisponde alla composizione di applicazioni lineari.
La moltiplicazione è definita soltanto se le matrici A e B sono rispettivamente di tipo M x P e P x N: in altre parole, il numero P di colonne di A deve coincidere con il numero P di righe di B. Il risultato è una matrice C di tipo M x N.
Esempio: siano A e B due matrici rispettivamente 3 x 4 e 4 x 2: tra queste si può effettuare la moltiplicazione A x B ed ottenere una matrice 3 x 2.
Le stesse matrici, però, non possono essere moltiplicate nel modo B x A, poiché le colonne di B non sono tante quante le righe di A.
Il prodotto di A di m righe e p colonne e B di p righe e n colonne è la matrice C = A\times B di dimensione m x n, il cui elemento di posizione (i,j) è dato dalla somma:
Quest'ultimo viene detto prodotto riga per colonna. Esempio:
Osservo che moltiplicando una matrice 2 x 3 per una 3 x 3 si ottiene una matrice 2 x 3.
1ª riga:
2ª riga:
A differenza dell'usuale moltiplicazione fra numeri, questa non è un'operazione commutativa, cioè AB è in generale diverso da BA, quando si possono effettuare entrambi questi prodotti.
Un caso particolare, ampiamente usato in algebra lineare per rappresentare le trasformazioni lineari (come rotazioni e riflessioni) è il prodotto tra una matrice m x n ed un vettore colonna n x 1, che viene chiamato anche prodotto matrice-vettore.
Le operazioni di somma e prodotto di matrici soddisfano tutte le proprietà usuali della somma e del prodotto di numeri, ad eccezione, nel caso del prodotto di matrici, della proprietà commutativa.
Sia 0 la matrice nulla, fatta di soli zeri (e della stessa taglia della matrice A, m x n ). Sia inoltre -A = (-1)A la matrice ottenuta moltiplicando A per lo scalare -1 . Valgono le relazioni seguenti, per ogni A, B, C matrici m \times n e, per ogni a,b numeri reali.
Proprietà della somma e del prodotto per uno scalare
- A + 0 = 0 + A = A (la matrice nulla è l'elemento neutro della somma)
- A + (-A) = 0 (esistenza di un opposto per la somma)
- (A + B) + C = A + (B+C) (proprietà associativa della somma)
- A + B = B + A (proprietà commutativa della somma)
- 1A = A (1 è l'elemento neutro del prodotto per uno scalare)
- (ab)A= a(bA) (proprietà associativa del prodotto per uno scalare)
- a(A + B)= aA + aB (proprietà distributiva della somma rispetto al prodotto per uno scalare)
Le prime 4 proprietà affermano che le matrici m x n formano un gruppo abeliano rispetto all'operazione di somma. Come mostrato sopra, il prodotto non è commutativo in generale.
Proprietà del prodotto fra matrici
- (AB)C = A(BC) (proprietà associativa del prodotto)
- (A+B)C = AC + BC; C(A+B) = CA + CB (proprietà distributiva della somma rispetto al prodotto)
Matrici quadrate
Fra le matrici, occupano un posto di rilievo le matrici quadrate, cioè le matrici n x n , che hanno lo stesso numero n di righe e di colonne.
Una matrice quadrata ha una diagonale principale, quella formata da tutti gli elementi a{i,i} con indici uguali. La somma di questi elementi è chiamata traccia.
L'operazione di trasposizione trasforma una matrice quadrata A nella matrice A{trasposta} ottenuta scambiando ogni a{i,j} con a{j,i} , in altre parole ribaltando la matrice intorno alla sua diagonale principale.
Una matrice tale che a{i,j} = a{j,i} è una matrice simmetrica. In altre parole, A è simmetrica se A = A{trasposta}.
Se tutti gli elementi che non stanno nella diagonale principale sono nulli, la matrice è detta diagonale.
La più importante matrice n x n è forse la matrice identità, I: è una matrice avente 1 su ogni elemento della diagonale e 0 altrove. La matrice è importante perché rappresenta l'elemento neutro rispetto al prodotto: infatti le matrici n x n possono essere moltiplicate fra loro, e vale (oltre a quelle scritte sopra) la proprietà seguente per ogni A:
Determinante
Un' importante quantità definita a partire da una matrice quadrata A è il suo determinante. Indicato con det(A), questo numero fornisce molte informazioni essenziali sulla matrice. Ad esempio, determina se la matrice è invertibile, cioè se esiste una matrice B tale che sia il prodotto matriciale AB che quello BA diano come risultato la matrice identità:
Il determinante è l'ingrediente fondamentale della regola di Cramer, utile a risolvere alcuni sistemi lineari.
Riepilogo
In definitiva, una matrice (di numeri reali (R)) è una tabella di m x n numeri disposti su m righe e n colonne.
I numeri che compaiono nella tabella si dicono elementi della matrice.
Matrici ed Excel
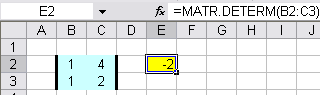
DETERMINANTE: Per calcolare il valore del determinante di una matrice quadrata si utilizza la formula =MATR.DETERM(matrice). In questo caso il risultato è un valore unico e non una matrice:
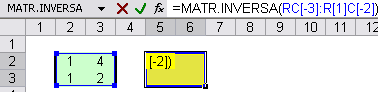
MATRICE INVERSA: Per ricavare la matrice inversa di una matrice assegnata si utilizza la formula =MATR.INVERSA(matrice).
In questo caso il risultato è una matrice. Per introdurre la formula si procede nel seguente modo:
- si seleziona l’area nella quale la nuova matrice verrà visualizzata;
- si introduce la formula nella prima cella in alto a sinistra della selezione;
Si completa l’immissione premendo contemporaneamente Shift + Control + Invio.
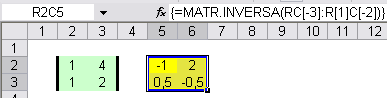
La formula è inglobata tra due parentesi graffe, aggiunte automaticamente dal programma, e viene visualizzato il risultato:
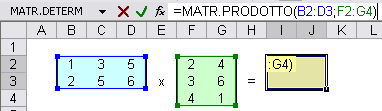
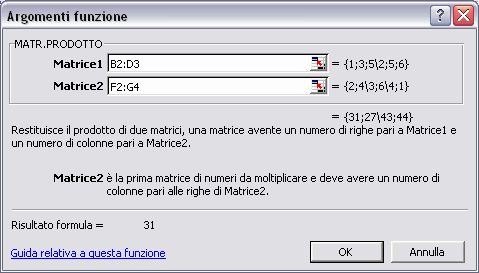
PRODOTTO: per calcolare il prodotto di due matrici si utilizza la formula =MATR.PRODOTTO(matrice1;matrice2). In questo caso il risultato è una matrice. Per introdurre la formula si procede nel seguente modo:
- Si seleziona l’area nella quale la nuova matrice verrà visualizzata;
- Si introduce la formula nella prima cella in alto a sinistra della selezione;
Si completa l’immissione premendo contemporaneamente Shift + Control + Invio.
La formula è inglobata tra due parentesi graffe, aggiunte automaticamente dal programma, e viene visualizzato il risultato.
Anche nel caso di procedura guidata occorre premere contemporaneamente Maiusc. + Control + Invio invece di utilizzare il mouse selezionando OK.
L’area di selezione destinata ad ospitare il risultato deve essere coerente con il numero di righe e di colonne restituite dalla funzione.
Se la funzione è inserita in una sola cella, invece che in un intervallo, viene restituito solo il primo elemento della matrice risultante.
La stessa cosa accade, al termine della procedura guidata, se si preme Invio o si seleziona il pulsante OK invece di premere contemporaneamente Shift + Control + Invio.
La soluzione dei sistemi lineari
Il sistema:
Può essere scritto nella forma matriciale:
Che ha soluzione:
Nella quale:
E' la matrice inversa della matrice dei coefficienti:
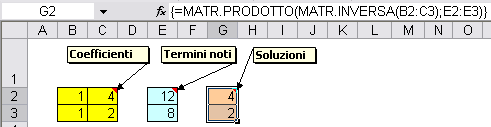
La formula da introdurre nel vettore delle soluzioni è quindi =MATR.PRODOTTO(MATR.INVERSA(matrice di coefficienti);vettore dei termini noti).
Le parentesi graffe nella formula sono state introdotte automaticamente da Excel, alla pressione simultanea dei tasti Shift + Control + Invio.
Sistemi non risolvibili
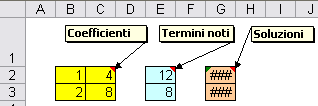
Perché il sistema sia risolvibile le equazioni devono essere tra di loro indipendenti; quando ciò non si verifica, non è possibile il calcolo della matrice inversa. In tale caso, le celle del vettore delle soluzioni sono riempite da Excel con il simbolo ####.
Ad esempio, il sistema:
presenta i coefficienti delle incognite della seconda equazione doppi rispetto a quelli della prima.
Con Excel si otterrebbe:
Il sistema precedente potrebbe essere riscritto nel modo seguente:
E’ evidente che l’assunto della prima equazione è in piena contraddizione con quello della seconda.
In termini di algebra matriciale, il sistema non è risolvibile se il determinante della matrice dei coefficienti presenta valore nullo.
La risoluzione dei sistemi lineari di equazioni con il metodo di Leibniz – Cramer
Risolvere il seguente sistema utilizzando il metodo di Leibniz-Cramer:
Come prima operazione si ordinano le equazioni, incolonnando opportunamente le incognite e spostando alla destra del segno di uguale il termine noto; se non è presente un'incognita, la si aggiunge moltiplicandola per il coefficiente zero.
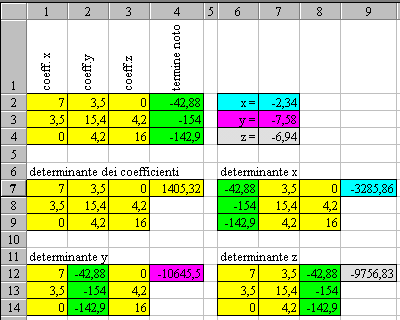
Con i coefficienti delle incognite si forma la matrice "determinante":
Con i termini noti si forma il vettore:
Secondo Leibniz (Gottfried Wilhelm von, 1646-1716 filosofo e scienziato tedesco) e Cramer (Gabriel, 1704-52 matematico svizzero) la soluzione del sistema è fornito dai seguenti rapporti di determinanti:
Il determinante al denominatore è costituito dai coefficienti dei termini noti:
Il determinante per il calcolo della x è ottenuto sostituendo la colonna dei coefficienti della x con il vettore dei termini noti:
Il determinante per il calcolo della y è ottenuto sostituendo la colonna dei coefficienti della y con il vettore dei termini noti:
Il determinante per il calcolo della z è ottenuto sostituendo la colonna dei coefficienti della z con il vettore dei termini noti:
In definitiva si ottiene:
Il calcolo con Excel
Inserimento dei dati
A partire dalla cella R2C1 si inseriscono i valori dei coefficienti e dei termini noti. Per maggiore chiarezza vengono colorate in giallo le celle con i valori dei coefficienti e in verde quelle contenenti i valori dei termini noti.
Costruzione del determinante dei coefficienti
Nella cella R7C1 si digita il simbolo = e si punta con il mouse nella cella R2C1, concludendo, infine, con la pressione del tasto Invio.
Si copia a destra la cella R7C1 trascinando di due posizioni il quadratino in basso a destra.
Si copiano in basso di due posizioni le celle da R7C1 (riga 7 colonna 1) a R7C3 (riga 7 colonna 3).
Calcolo del determinante
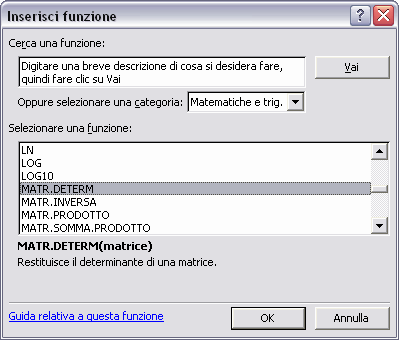
Dopo essersi posizionati nella cella R7C4 si fa clic sul pulsante per l'inserimento delle funzioni di Excel. Dalla finestra di dialogo Incolla funzione si sceglie la categoria Matematiche e trig. e il Nome funzione MATR.DETERM.
Come argomento della funzione si inserisce il rettangolo di celle da R7C1 a R9C3.
La formula risultante è:
=MATR.DETERM(RC[-3]:R[2]C[-1])
Costruzione del determinante x
Si ripete il procedimento già seguito per la creazione del determinante dei coefficienti, partendo questa volta dalla cella R7C6. Per sostituire la prima colonna del determinante con quella dei termini noti si digita il simbolo = nella cella R7C6, si fa clic sulla cella R2C4 ed, infine si batte Invio; la formula così ottenuta viene ricopiata in basso di due righe.
Il valore del determinante x si calcola con la stessa procedura già esaminata a proposito del calcolo del determinante dei coefficienti.
Costruzione dei determinanti y e z
Si ripete il procedimento seguito per il determinante x apportando la seguente variazione: le colonne dei coefficienti da sostituire con quella dei termini noti sono quelle relative alle y e alle z.
Calcolo dell'incognita x
Nella cella R2C7 si digita il simbolo = , si fa clic sulla cella R7C9, si inserisce il simbolo /, si fa clic sulla cella R7C4 ed infine si batte Invio.
La formula risultante è:
R[5]C[2]/R[5]C[-3]
Calcolo delle incognite y e z
Si ripete il procedimento già visto per l'incognita x partendo dalle celle R8C9 e R10C9 ed inserendo il valore dei rispettivi determinanti y e z nella formula.
Perché il sistema sia risolvibile le equazioni devono essere tra di loro indipendenti; se ciò non si verifica, il valore del determinante dei coefficienti è nullo. Poiché tale determinante è inserito al denominatore nelle formule per il calcolo delle incognite conduce ad un errore.
E' opportuno perciò l'inserimento di un controllo che evidenzi un messaggio nel caso il sistema non sia risolvibile; questo obiettivo può essere raggiunto mediante l'uso della funzione SE(). In altri termini: se il valore del determinante dei coefficienti è diverso da zero, si calcola il valore dell'incognita altrimenti si visualizza un messaggio del tipo "equazioni linearmente dipendenti".
La formula per il calcolo della x può essere così riscritta:
=SE(R[5]C[-3]<>0;R[5]C[2]/R[5]C[-3];"eq. linearm. dipendenti")
Download
NOTA: il download è permesso ai soli utenti registrati od autenticati su HeelpBook. Perdonate l'inconveniente.
[wpfilebase tag="file" id=168 /]