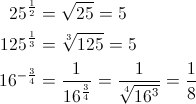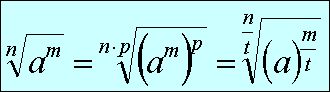To totally unlock this section you need to Log-in

In matematica, la radice n-esima o radicale n-esimo (con n diverso da 0) di un numero reale a, scritto come , è un numero reale b tale che : in generale si definisce radice n-esima di un numero reale, quel numero che elevato alla n da come risultato il numero dato.

In simboli, se , dalla definizione di prima otteniamo:

L'unica proprietà che hanno i radicali è la proprietà invariantiva, che però richiede una dimostrazione.

Teorema: Il valore di un radicale in non cambia se si moltiplicano l'indice del radicale e l'esponente del radicando per uno stesso numero naturale positivo.

Cioè:

Bisogna dimostrare questa data proprietà:

Eleviamo alla np il primo membro:

Eleviamo ora il secondo membro alla np:

Per la proprietà transitiva dell'uguaglianza si deduce che è:

da cui, si ottiene l'uguaglianza delle basi positive di tali potenze aventi lo stesso esponente np e si ha:

Caso della potenza frazionaria

Il radicale può essere descritto come un elevamento a potenza frazionaria, ovvero un radicale sarà equivalente al numero sotto radice elevato ad una frazione uguale al grado del radicale stesso:

E quindi:

I due casi di radicale

Per la definizione corretta di radicale di un numero, o radice n-esima di un numero reale a, ovvero appartenente all'insieme dei numeri reali R, bisogna distinguere due casi in particolare:

Se n è dispari: ovvero il numero posto al di sopra del simbolo di radice, si dice radice n-esima di a quel numero b che elevato ad al numero naturale n ci restituisce a, ovvero:

Se n è pari: si dice radice n-esima di a quel numero positivo b che elevato ad n ci restituisce il valore a, cioè:

In entrambi i casi: a si chiama radicando, n si dice indice di radice e √ è detto simbolo di radice. Per fissare le idee, la radice terza (il valore n sulla radice in questo caso sarà 3) di 8 è 2 e scriveremo:

Ci si potrebbe chiedere perché, nel caso in cui n è pari, abbiamo richiesto che b sia positivo. Il motivo non è difficile da capire e consigliamo a tutti di leggere le prossime righe perché è un errore in cui cadono molti. Supponiamo ad esempio di voler determinare la radice quadrata del numero 4; possiamo osservare che, per com'è definita la potenza di un numero, risulta:

Esistono perciò due numeri (2 e -2) il cui quadrato è 4. L'operazione di estrazione di radice con indice pari (in questo caso con indice 2) sarebbe quindi definita in modo equivoco se non si precisasse quale numero scegliere come radice di 4. Per questo motivo si conviene che:

e non, come ritengono molti:

Campo di esistenza dei radicali

Prima di tutto c'è da apprendere questo concetto: in R , ovvero nel campo dei numeri reali, i radicali con indice pari esistono se e solo se il radicando è maggiore o uguale a 0, mentre i radicali con indice dispari esistono sia quando il radicando è positivo sia quando è negativo sia quando è nullo.

Le condizioni di esistenza dei radicali, o campo di esistenza, (abbreviato si indica con C.E.) sono l’insieme dei valori (numeri) da attribuire alle variabili (ossia le lettere) del radicando, affinché il radicale esista (o abbia significato).

Proprio perché dal C.E. dipende l’esistenza o meno dei radicali, la ricerca del C.E. si fa sempre e subito, cioè all’inizio di ogni tipo di esercizio con i radicali. In un esercizio di ricerca del C.E. dei radicali, non si può fare nessun tipo di operazione nel testo poiché non sappiamo se tale radicale esiste o no.

Ma ora passiamo alle cose più importanti: come si calcola il C.E. di un radicale algebrico?

Per poter fare il C.E. di un radicale algebrico è necessario aver studiato le disequazioni. Infatti nei radicali con indice pari il C.E. è formato da tutti i numeri che rendono positivo o nullo, ossia non negativo (≥0), il radicando.

In tal caso il C.E. corrisponde alla soluzione della disequazione: radicando ≥0, ossia deve risolvere una disequazione. Ben diverso, e anche più semplice, è il caso in cui i radicali hanno l’indice dispari, perché il radicando può essere positivo, negativo o nullo, e quindi non si deve risolvere una disequazione; il C.E. è tutto R, tranne nel caso in cui i radicandi sono frazionari perché dobbiamo togliere dal C.E. i valori che annullano i denominatori.

In definitiva, se l'indice della radice è pari (maggiore di zero) allora il radicando deve essere maggiore o uguale a zero; se invece l'indice della radice è dispari allora il radicando può avere segno qualsiasi. Ad esempio la radice quadrata di un numero negativo non è definita, mentre la radice cubica (ovvero alla potenza di 3) esiste sempre. Per identificare meglio questa situazione osservate l'immagine seguente:

Radicali come potenze con esponente fratto

È utile sapere che esiste un ulteriore modo per indicare la radice n-esima. Vale infatti la seguente relazione:

Tramite la quale possiamo esprimere la radice ennesima tramite potenze con esponente razionale. Possiamo generalizzare la precedente formula come:

Se volessimo esprimere con semplici parole quest'ultima relazione diremmo: l'indice del radicale diventa il denominatore dell'esponente della potenza mentre l'esponente del radicando diventa il numeratore della potenza.

Attenzione agli esponenti negativi

Per definizione si pone: , ovvero bisogna porre al denominatore il valore elevato a potenza frazionaria negativa, e quindi rieseguire la definizione di potenza frazionaria al numero sottostante, rendendolo di fatto un radicale "esplicito" al denominatore. Di seguito sono mostrati alcuni esempi di potenze frazionarie positive e, l'ultima, una potenza frazionaria negativa:

Proprietà dei radicali

Somma e differenza di radicali: possiamo sommare o sottrarre radicali simili,cioè quei radicali che hanno stesso indice e stesso radicando. Nel caso della somma, ma analogamente anche per la sottrazione, si otterrà un nuovo radicale che avrà come radice la stessa radice e come parte numerica la somma dei coefficienti. Vediamo un esempio:

Evidenziamo i termini simili utilizzando due colori:

Sommiamone i coefficienti:

In definitiva:

Prodotto di radicali con lo stesso indice

Possiamo moltiplicare o dividere , in modo molto semplice, radicali che hanno lo stesso indice di radice.
Si includono i radicandi in un'unica radice, e si eseguono la moltiplicazione o la divisione. Per il prodotto di due radici si otterrà una radice che avrà indice inalterato (rimarrà lo stesso) e per radicando (ovvero i numeri al di sotto del simbolo di radice) il prodotto dei due (o più) radicandi coinvolti nella moltiplicazione:

Ricordatevi sempre che le formule possono essere lette anche al contrario. In tal caso la precedente formula può essere riespressa così:

"La radice n-esima di un prodotto coincide con il prodotto delle radici n-esime di ciascun fattore."

Quoziente di due radicali con lo stesso indice

Il quoziente di due radici aventi lo stesso indice è una radice che ha per radicando il quoziente dei radicandi e per indice lo stesso indice.

Leggendo la formula al contrario: la radice del quoziente è il quoziente delle radici. :)

NOTA: se le radici hanno indice diverso, la moltiplicazione o la divisione si può eseguire,
ma occorre dapprima calcolare il minimo comune indice (m.c.i.) come il minimo comune multiplo fra gli indici, e poi eseguire l’operazione nel modo seguente: si divide il valore del m.c.i. per l’indice della prima radice ed il quoziente ottenuto è la potenza al quale occorre elevare il radicando della prima radice, e così si procede con le altre radici, allo stesso modo.

Prima di osservare con attenzione quest'ultimo caso abbiamo la necessità di enunciare una proprietà importante per quanto riguarda i radicali: la proprietà invariantiva.

Proprietà invariantiva dei radicali

Definizione: moltiplicando o dividendo l’indice del radicale e l’esponente del radicando per uno stesso numero naturale, diverso da 0, il valore del radicale non varia. In formule matematiche avremo:

O, più in generale:

La formula può anche essere letta al contrario, da destra a sinistra, se risulta necessario. Ci si potrebbe chiedere come mai è richiesto che il radicando sia non negativo (ovvero l'elemento sotto il simbolo di radice), la risposta a questa domanda è che se prendessimo in considerazione, per questa proprietà, radicandi negativi potremmo giungere a contraddizioni inaspettate:

La proprietà invariantiva dei radicali ci consente di moltiplicare/dividere tra loro radici con indici diversi, in modo da ricondurci a radici che hanno lo stesso indice.

Riduzione di due radicali allo stesso indice

Utilizzando la sopracitata proprietà invariantiva si possono eseguire delle riduzioni importanti della complessità dei radicali, e per far ciò dovremo considerare due radici con due indici distinti , con , quindi calcolare il minimo comune multiplo tra i due esponenti n ed m, che diventerà l'indice comune a tutte le radici, ed infine dividere il nuovo indice per ciascun indice delli radici, il cui quoziente diventerà l'esponente del radicando. Otterremo nuove radici equivalenti a quelli originari.

Ad esempio, prendiamo le seguenti due radici ad esponenti differenti e ci calcoliamo molto semplicemente il minimo comune denominatore:

Il minimo comune multiplo tra 3 e 4 è 12 e diventerà il nuovo indice delle radici:

Giunti a questo punto dovremo dividere 12 per 3 ed otterremo 4 che è l'esponente del primo radicando, analogamente, dividiamo 12 per 4 ed otterremo 3 che è l'esponente del secondo radicando: .

Con la riduzione allo stesso indice possiamo calcolare sia la moltiplicazione che la divisione tra due radicali con indici diversi, usufruendo delle proprietà successive.

Moltiplicazione e divisione di radicali con indici diversi

Il prodotto ed il quoziente di radici con indici diversi sarà necessario dapprima ridurre allo stesso indice entrambi i radicali, dopodiché si utilizzeranno le proprietà di prodotto e quoziente tra radicali.

Riduciamo i radicali allo stesso indice:

Utilizzando la proprietà dei radicali riguardo il prodotto:

Potenza di un radicale

La potenza di un radicale non è altro che un radicale che ha come indice lo stesso indice iniziale e come radicando, ovvero l'elemento sotto il simbolo di radice, elevato al numero che esprime la potenza del radicale dato, ovvero vale la relazione:

Possiamo quindi dire che: la potenza m-esima di una radice che ha indice n e radicando a è una radice che ha per indice n e per radicando la potenza am.

Radice di radice

Una delle operazioni che tende a spaventare maggiormente gli studenti è il calcolare il radicale di una radice.

Per risolvere un'operazione di questo tipo devi eliminare la prima radice, quella più esterna, scrivendo solamente la seconda (quella posta inizialmente sotto il radicale), riscrivere il radicando senza modificarlo e cambiare l'esponente della radice, semplicemente moltiplicando tra loro quelli delle due radici iniziali.

La radice m-esima di una radice n-esima con radicando a è una radice che ha per indice il prodotto degli indici, m x n, e per radicando a:

Trasporto di un fattore dentro il segno di radice

E' necessario partire osservando con estrema attenzione il fattore che ti viene chiesto di "trasportare sotto la radice". Tale fattore, infatti, deve obbligatoriamente essere positivo, e quindi maggiore di "0", ovvero preceduto dal segno più (stiamo infatti operando con numeri razionali e quindi reali).

In caso contrario, e può succedere che ti venga chiesto, dovrai semplicemente dire che l'operazione è "impossibile" e non può, quindi, essere eseguita.

Un numero negativo non può essere messo sotto una radice, per il semplice motivo che la sua operazione inversa è impossibile (nessun numero elevato al quadrato può dare un numero negativo).

Quando un radicale è moltiplicato per un fattore positivo si può portare tale numero dentro la radice dopo averlo elevato ad una potenza uguale all'indice della radice. In questo processo l'indice della radice non subisce alcuna alterazione: se è cubica, ad esempio, quindi con indice 3, rimarrà cubica.

E se il fattore fuori la radice è negativo? Poco male! Si trasporta dentro il segno di radice il numero senza il segno lasciando il meno fuori:

Trasporto di un fattore fuori il segno di radice

Per risolvere questi esercizi, bisogna prima riscrivere i termini sotto radice sotto forma di potenze, per poter poi portare fuori, ove possibile, i termini; ed infine fare le somme algebriche tra i termini. Per ricavare la proprietà utilizzata per questo tipo di operazione si può partire dall'analisi della proprietà che consente di trasportare un fattore sotto il segno di radice:

L'uguaglianza appena visionata permette di trasportare fuori dalla radice un fattore, ovviamente positivo, del radicando che sia una potenza con esponente uguale (ad esempio se la radice è cubica, l'esponente del fattore sotto radice dovrà almeno essere 3) all'indice della radice.

Più in generale, il trasporto fuori dal segno di radice di un fattore vale se all'interno del radicando c'è un fattore che sia una potenza con esponente uguale o multiplo del radicando, ovvero:

Ogni fattore all'interno del radicando che abbia un esponente uguale o maggiore dell'indice della radice può essere trasportato fuori. Osserviamo i seguenti esempi:

L'esponente del 2 è pari a 5 ed è maggiore dell'indice della radice. Scomponendo l'esponente in una moltiplicazione da fattori elevati a potenza (che porta alla somma degli esponenti) otterremo: