The two most common/confused words in digital communication – Bit rate and Baud rate. Generally, communication is concerned with transmission of data. In digital communication, there are two entities that are needed to carry out communication – the data to be transmitted and the signal over which the data is transmitted.
Now, we have two entities to be worried about – the data and the signal. The most common misconception is that most people think both travel at the same speed: no, this is wrong.
The difference
Digital data is very different from digital signal. The process of converting digital data to digital signal is called as line coding.
Now, to discriminate between data and signal, data is what we need to send. But signal is what we can send.
So, signal is the carrier which carries data. Also, keep in mind that the smallest entity of the data, that can represent a piece of information is called data element and shortest meaningful unit of a signal is called signal element.
Consider this as in the following scenario: consider a train. Each carriage is a signal element. Each passenger inside the train is a data element. The train as a whole is a signal and all passengers together represent a data.
Data rate and Signal rate
- Data rate – Number of data elements transmitted per second.
- Signal rate – Number of signal elements transmitted per second.
Now, the unit of data rate is bit rate. And the unit of signal rate is pulse rate/ modulation rate/ baud rate or simply baud. From the previous example, we can see that, a carriage in a train can carry more than one person. So, if you consider the number of person is more than one per carriage, you can say that bit rate is greater than baud rate for the signal.
Calculating the baud rate
Baud rate is calculated using the below formula:
Here: N is the bit rate (in bps - bits per second) and r is the number of data elements carried by each signal element. Here r must be as great as possible for better efficiency (stuff more people in a carriage :P).
From the above text, it is clearly inferred that the bit rate must be greater than the baud rate for higher efficiency. The aim is to transmit as many data element as possible in a signal element. There are different methods to do this which are collectively called as line coding schemes.Some of the popular line coding schemes are: Non-return to zero (NRZ), Manchester, Alternate mark inversion (AMI) and also multi level schemes are available.
Few Examples
Consider the below figures:
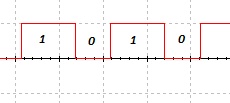
Here, the data rate (bit rate) and signal rate (baud) are same and r is one (one bit for each signal). One data element rides on one signal element (analogous to one person per carriage in a train).
And in this image, you can see that there are two data elements transmitter per signal element. In other words, the bit rate is higher than the baud rate. (Analogous to two passengers per carriage in a train) and here r is two. Hence baud rate is one half of bit rate.
And the next time, when you define the baud rate – its number of signal elements per second and not number of bits per second.
Digital Communication Methods
A communications system may be digital either by the nature of the information (also known as data) which is passed or in the nature of the signals which are transmitted. If either of these is digital then for our purposes it is considered to be a digital communications system. There are four possible combinations of data and signal types:
- Analog data, analog signal.
- Digital data, analog signal.
- Analog data, digital signal.
- Digital data, digital signal.
Digital Data with Analog Signals
This method is used to send computer information over transmission channels that require analog signals, like a fiber optic networks, computer modems, cellular phone networks, and satellite systems. In each of this systems, an electromagnetic carrier wave is used to carry the information over great distances and connect digital information users at remote locations.
The digital data is used to modulate one or more of the parameters of the carrier wave. This basic process is given the name "shift-keying" to differentiate it from the purely analog systems like AM and FM. As with analog modulation, there are three parameters of the carrier wave to vary and therefore three basic types of shift keying:
- Amplitude Shift Keying (ASK)
- Frequency Shift Keying (FSK)
- Phase Shift Keying (PSK)
In ASK, the amplitude of the carrier wave is changed instantly based on the digital data, without changing the frequency and phase of the carrier wave.
In FSK, the frequency of the carrier wave is alone changed based on the instantaneous value of the digital data, keeping the amplitude and phase constant.
In PSK, the phase of the carrier wave is changed based on the digital data that is to be encoded, without changing the amplitude and carrier.
To understand these modulation techniques, let us take the very basic version of these techniques, namely Binary-ASK, Binary-FSK and Binary-PSK or BPSK.
Since there are only two different types of symbols in binary data, namely 0 and 1, the encoded analog signal would either have two different amplitudes (ASK) or two different frequencies (FSK) or two different phases (PSK).
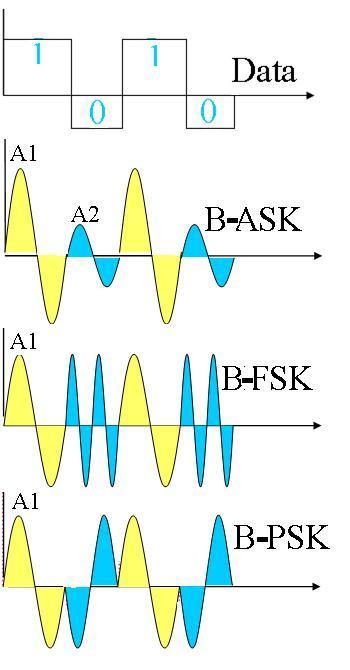
The following diagram given below illustrates the three digital modulation techniques for encoding the same digital data pattern (1010).
NOTE: in the following example the baud rate will be the same of the bit rate.
In the diagram, for encoding the same digital binary stream 1010:
- BASK uses two different amplitudes, namely A1 for encoding a binary 1 and A2 for encoding a binary 0, without changing the carrier wave’s frequency and phase.
- BFSK uses two different frequencies (number of cycles per second), for representing binary 1 and binary 0, without changing the carrier wave’s amplitude and phase. While a binary 1 is represented by a single cycle of the wave in one bit interval, a binary 0 is represented by a wave with two cycles in one bit interval. The amplitude and phase of the carrier wave is unchanged.
- BPSK uses two different phases for representing binary 1 and binary 0, without chaning the carrier wave’s amplitude and frequency. While a binary 1 is represented by a normal sine wave, a binary 0 is represented by a similar sine wave shifted in phase by 180 degree.
Multi-Level ASKs, FSKs, PSKS
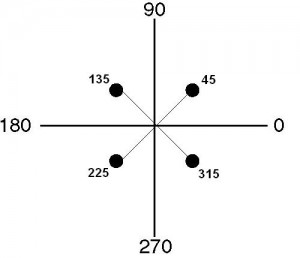
Generalizing the above line encoding techniques, by having multiple signalling levels/values (instead of two in binary), it is possible to have different line coding techniques. For example, 2-level, 4-level, 16-level ASKs, FSKs or PSKs etc. The diagram given below illustrates a 4-level PSK:
NOTE: The 4-level PSK signaling will enable a data rate doubled in respect of baud rate.
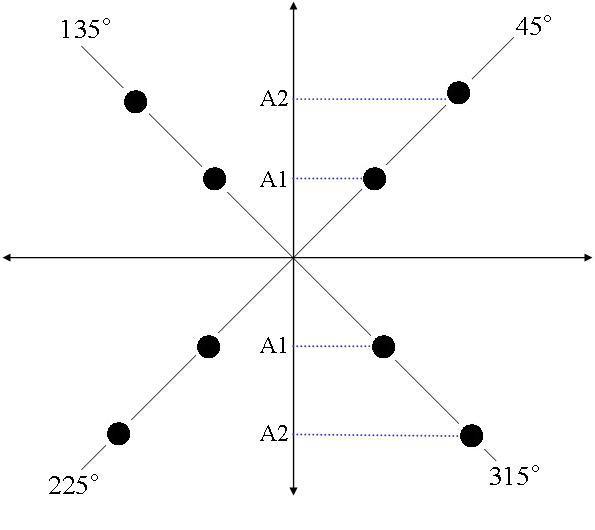
The above diagram format is named as constellation diagram. It is similar to the polar coordinate system, where the angle of a vector represents the phase and the length of the vector represents the amplitude.
Each dot represents a specific value of the signal or it represents a unique symbol. In this example of 4-level PSK, there are 4 different symbols, each represented by dots. The 4 symbols have different phase values, while having the same amplitude. As seen from the above diagram, in this particular example of 4-level PSK, a sine wave with 4 different phases, namely with degrees 45, 135, 225 and 315 are used to represent four different symbols.
If data encoded is to be binary, then these 4 symbols could be 00, 01, 10 and 11. Thus using one signal value (or symbol), two binary digits could be encoded in this scheme. Therefore, in 4-level PSK, data rate (number of bits per second) that can be sent is double when compared to BPSK, for the same symbol rate.
Combining ASK and PSK (QAM)
Another common approach to increase the bit rate is to simultaneously use both ASK (different amplitudes) and PSK (different phases), without changing the frequency of the carrier wave. Such techniques are referred to as QAM (Quadrature Amplitude Modulation). The figures given below illustrate two such examples of combining ASK and PSK.
QAM-8 uses two different Amplitudes and four phases thereby giving eight different symbols. Since there are 8 different symbols, each symbol could be used to represent 3 binary digits (for e.g. symbol1 represents 000, symbol2 represents 001, … symbol8 represents 111), thereby giving a data rate that is 3 times that of the symbol rate.
QAM-16 uses four amplitudes and four phases, therey giving sixteen different symbols. Using a similar logic, QAM-16 can represent 4 binary digits per symbol and hence the data rate of QAM-16 is four times that of the symbol rate.
Using similar techniques with more values of amplitudes and phases, higher data rates can be achieved.
One thing to be noted is that more number of symbols means the overall complexity of processing increases at the sender and receivere. Especially, the complexity is more at the receiver as it does not know the incoming symbols and hence needs the capability to instantaneously decode between different symbols that are coming at line rate.
Another approach that is commonly used is to combine these modulation techniques with channel multiplexing techniques like FDM, TDM etc. to achieve even more higher data rates.
Bit and Baud Rates
In general, for multi-level modulation techniques, if there are “N” number of symbols and if the symbol rate (number of symbols that can be transmitted on the link per second) is S, then the data rate (D)(number of bits per second that can be transmitted on the link) is D= S * log N, where the base of the log is 2.
While the symbol rate is generally known as the baud rate, the data rate is known as the bit rate.